Suite Aliquote – Bac Pratique 2014 [ Algorithme + Python ]

Sujet bac informatique pratique 2014 (Bac scientifique)
Une suite Aliquote est une suite d’entiers dans laquelle chaque terme Un (avec n>0) est la somme des diviseurs propres du terme qui le précède (Un-1). Quand la suite atteint la valeur 1, elle s’arrête car 1 ne possède pas de diviseurs propres.
N.B : les diviseurs propres d’un nombre sont tous ses diviseurs sauf lui-même.
Exemple : Pour U0 les termes de la suite Aliquote de 12 seront calculés comme suit :
Les diviseurs propres de 12 sont 1,2,3,4 et 6 donc U1=1+2+3+4+6=16
Les diviseurs propres de 16 sont 1,2,4 et 8 donc U2=1+2+4+8=15
Les diviseurs propres de 15 sont 1,3 et 5 donc U3=1+3+5=9
Les diviseurs propres de 9 sont 1 et 3 donc U4=1+3=4
Les diviseurs propres de 4 sont 1 et 2 donc U5=1+2=3
Les diviseurs propres de 3 sont 1 donc U6=1
La suite Aliquote de 12 est 12 16 15 9 4 3 1
Travail demandé :
Ecrire un programme Python qui permet de saisir U0 avec U0≥10 et d’afficher les termes de la suite et afficher si la suite est Aliquode ou non.
N.B : Le calcul des termes de la suite s’arrête dans l’un des deux cas suivants :
Lorsqu’on atteint la valeur 1 et dans ce cas la suite est Aliquote.
Lorsque la valeur d’un nouveau terme est égale à la valeur de son précédent (Un=Un-1) et dans ce cas la suite n’est pas Aliquote.
Solution Algorithmique
Pour résoudre ce problème, voici le principe de l'algorithme à suivre :
1. Saisie de la valeur initiale U0
Demander à l'utilisateur de saisir une valeur initiale U0 avec la contrainte que U0 doit être supérieur ou égal à 10.
2. Calcul des termes de la suite
Initialiser la valeur actuelle de la suite Un à U0.
Boucle de calcul des termes :
Tant que Un n'est ni égal à 1 ni égal à la valeur précédente Un-1 :
a) Calculer les diviseurs propres de Un.
b) Faire la somme des diviseurs propres pour obtenir le nouveau terme Un+1.
c) Mettre à jour la valeur de Un avec Un+1.
3. Conditions d'arrêt
- Si la valeur de Un devient 1, la suite est Aliquote. Afficher la suite complète et indiquer qu'elle est Aliquote.
- Si la valeur de Un est égale à Un-1 (c'est-à-dire que la suite devient constante), arrêter le calcul. Afficher la suite complète et indiquer qu'elle n'est pas Aliquote.
4. Affichage des résultats
Afficher tous les termes de la suite calculée.
Indiquer si la suite est Aliquote ou non.
Dans cet algorithme, On va utiliser deux fonctions et une procédure :
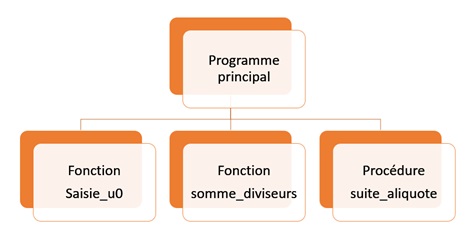
Algorithme du programme principal
|
1 2 3 4 5 |
Algorithme test_suite_aliquote Debut u0<-saisie_u0() suite_aliquote(u0) Fin |
Déclaration des objets
Objet | Type / Nature |
u0 | entier |
La fonction saisie_u0
Cette fonction retourne un entier >= 10 saisi par l'utilisateur.
|
1 2 3 4 5 6 7 8 9 10 |
fonction saisie_u0():entier Début Ecrire('donner un entier >= 10 ') lire (n) Tant que n<10 faire Ecrire('donner un entier >= 10 ') lire (n) Fin tant que retourner n Fin |
Déclaration des objets
Objet | Type / Nature |
n | entier |
La fonction somme_diviseurs
Cette fonction calcule la somme des diviseurs propres de l'entier n excepté lui-même.
|
1 2 3 4 5 6 7 8 9 10 |
fonction somme_diviseurs(n:entier):entier Début s<-0 Pour i de 1 à n div 2 faire Si (n mod i=0) alors s<-s+i Fin si Fin pour retourner s Fin |
Déclaration des objets
Objet | Type / Nature |
i | entier |
s | entier |
La procédure somme_diviseurs
Cette procédure calcule la somme des diviseurs propres de l'entier n excepté lui-même.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 |
Procedure suite_aliquote(u:entier) Début i<-0 Ecrire('U',i,'=',u) u<-somme_diviseurs(u) v<-0 Tant que (u>1) et (u!=v) faire v<-u i<-i+1 Ecrire('U',i,'=',u) u<-somme_diviseurs(u) Ecrire('U',i,'=',u) Fin tant que Si (u=1) alors Ecrire('cette suite est Aliquode') Sinon Ecrire('cette suite est non Aliquode') Fin si Fin |
Déclaration des objets
Objet | Type / Nature |
i | entier |
u | entier |
v | entier |
Solution en Python
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 |
def saisie_u0() : n=int(input('donner un entier >= 10: ')) while n<10 : n=int(input('donner un entier >= 10: ')) return n def somme_diviseurs(n): s=0 for i in range(1,n//2+1): if (n % i==0): s=s+i return s def suite_aliquote(u): i=0 print('U',i,'=',u) u=somme_diviseurs(u) v=0 while (u>1) and (u!=v): v=u i=i+1 print('U',i,'=',u) u=somme_diviseurs(u) print('U',i,'=',u) if (u==1): print('cette suite est Aliquode') else: print('cette suite est non Aliquode') #programme principal u0=saisie_u0() suite_aliquote(u0) |
Exécution du programme

Solution en Python et Designer QT
Pour créer une application en Python pour saisir U0 avec U0≥10 et d’afficher les termes de la suite et afficher si la suite est Aliquode ou non en utilisant Qt Designer pour l'interface graphique, suivez ces étapes :
1- Créer l'interface graphique avec Qt Designer
a- Ouvrez Qt Designer et créez un nouveau fichier de type Main Window.
b- Ajoutez ces widgets:
QLineEdit nommé 'u' pour entrer un entier >=10.
QPushButton nommé 'test_bt' pour exécuter le module suite_aliquote.
QLabel nommé 'msg' pour afficher un message d'erreur.
QLabel nommé 'resultat' pour afficher les termes de la suite et afficher si la suite est Aliquode ou non.
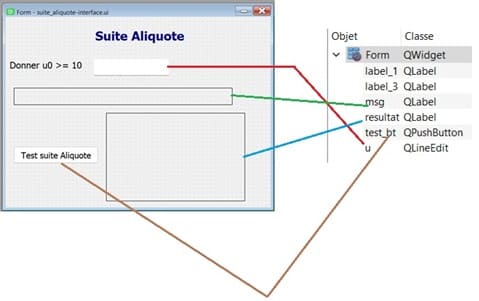
Enregistrez le fichier avec l'extension .ui, par exemple suite_aliquote-interface.ui.
2- Créer le script Python pour l'application
Voici un exemple de script Python qui utilise l'interface graphique générée par Qt Designer.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 |
from PyQt5.uic import loadUi from PyQt5 import QtCore, QtGui from PyQt5.QtWidgets import * from PyQt5 import QtCore, QtGui, QtWidgets app = QApplication([]) windows = loadUi ("suite_aliquote-interface.ui") def somme_diviseurs(n): s=0 for i in range(1,n//2+1): if (n % i==0): s=s+i return s def suite_aliquote(): i=0 liste='' u=int(windows.u.text()) if u>=10 : liste=liste+'U'+str(i)+'='+str(u)+'\n' u=somme_diviseurs(u) v=0 while (u>1) and (u!=v): v=u i=i+1 liste=liste+'U'+str(i)+'='+str(u)+'\n' u=somme_diviseurs(u) print('U',i,'=',u) liste=liste+'U'+str(i)+'='+str(u)+'\n' if (u==1): liste=liste+'cette suite est Aliquode' else: liste=liste+'cette suite est non Aliquode' windows.resultat.setText(liste) else: windows.msg.setText('Donner u>=10') windows.test_bt.clicked.connect(suite_aliquote) windows.show() app.exec_() |
Exécution du programme
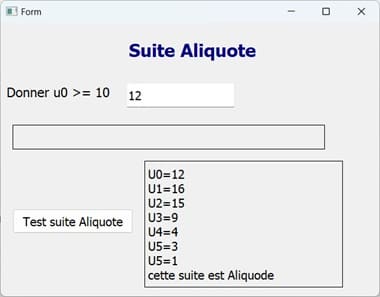
Vous pouvez voir aussi :
1) des exercices sur les chaînes des caractères
2) des exercices sur les tableaux
3) des sujets Bac pratique
4) des sujets Bac théorique
1 commentaire
crispy 16-02-2525
tnjmou tkhdmoha b fichier binaire w ysir l affichage 3la fichier texte khater ml9itech solution
laisser un commentaire
Tutoriels récents
Tutoriels populaires

Tutoriels plus commentés