PGCD de deux entiers – Bac Pratique 2015 [ Algorithme + Python ]

Sujet bac informatique pratique 2015 (Bac scientifique)
La décomposition du PGCD(A,B) en facteurs premiers (avec A≥2 et B≥2) est le produit des facteurs premiers apparaissant à la fois dans la décomposition de A et de B munis de plus petit des exposants trouvés dans la décomposition de A et de B.
N.B : On dit qu’un nombre a admet le nombre b comme facteur premier lorsque b est un nombre premier qui divise a.
Ecrire un programme Python qui permet de saisir deux entiers a et b (10≤a≤b), de chercher la décomposition en facteurs premiers du PGCD(A,B) en utilisant le principe ci-dessus.
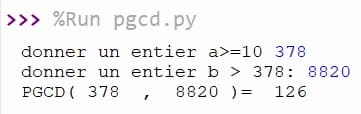
Exemple : Pour A=378 et B=8820
Liste des facteurs premiers de A=378=2*33*7.
Liste des facteurs premiers de B=8820=22*32*5*72.
Alors le programme affiche : PGCD(378, 8820)= 2*33*7=126
Solution Algorithmique
1. Saisie des deux entiers A et B
L'algorithme commence par demander à l'utilisateur de saisir deux entiers A et B, tels que 10≤A≤B.
2. Décomposition en facteurs premiers
a) Pour chaque entier A et B, on effectue une décomposition en facteurs premiers.
b) Cela implique de diviser successivement A et B par les nombres premiers croissants (commençant par 2) jusqu'à obtenir 1.
c) Pour chaque nombre qui divise A ou B sans reste, on l'enregistre comme un facteur premier et on continue avec le quotient obtenu.
d) Chaque facteur est enregistré avec son exposant, c'est-à-dire le nombre de fois qu'il divise le nombre en question.
3. Trouver les facteurs communs avec le plus petit exposant
a) L'algorithme identifie les facteurs premiers communs aux deux nombres A et B.
b) Pour chaque facteur commun, il sélectionne le plus petit exposant trouvé dans la décomposition de A et B.
4. Calcul du PGCD à partir des facteurs communs
Le PGCD est alors le produit des facteurs premiers communs, chacun élevé au plus petit exposant trouvé dans les décompositions respectives de A et B.
5. Affichage de la décomposition du PGCD
a) L'algorithme affiche la décomposition en facteurs premiers du PGCD avec les facteurs communs et leurs exposants.
b) Il affiche ensuite la valeur numérique du PGCD.
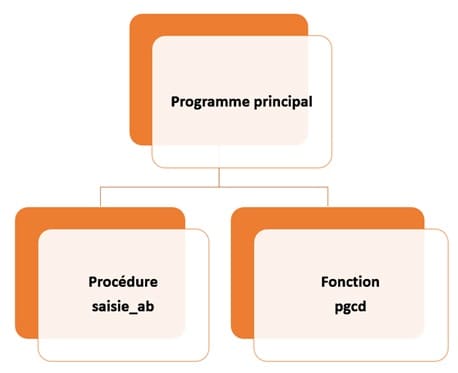
Dans cet algorithme, On va utiliser deux fonctions :
|
1 2 3 4 5 |
Algorithme calcul_pgcd Debut saisie_ab() Ecrire('PGCD(',a,' , ',b, ')= ',pgcd(a,b)) Fin |
Déclaration des objets
| Objet | Type / Nature |
|---|---|
| a | entier |
| b | entier |
La procédure saisie_ab
Cette procédure saisit deux entiers m et n tel que 10≤a
Déclaration des objets La fonction pgcd Cette fonction calcule le PGCD des deux entiers a et b Déclaration des objets pentier Exécution du programme Pour créer une application en Python pour calculer le PGCD de deux entiers en utilisant Qt Designer pour l'interface graphique, suivez ces étapes : a- Ouvrez Qt Designer et créez un nouveau fichier de type Main Window. b- Ajoutez ces widgets: Enregistrez le fichier avec l'extension Voici un exemple de script Python qui utilise l'interface graphique générée par Qt Designer. Exécution du programme Vous pouvez voir aussi :
Objet
Type / Nature
a
entier
b
entier
Objet
Type / Nature
i
entier
p
entier
Solution en Python

Solution en Python et Designer QT
1- Créer l'interface graphique avec Qt Designer
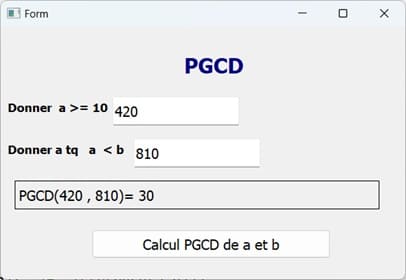
QLineEdit nommé 'a' pour entrer un entier >=10.QLineEdit nommé 'b' pour entrer un entier b >a.QPushButton nommé 'pgcd_bt' pour exécuter le module calcul_pgcd.QLabel nommé 'msg' pour afficher un message d'erreur et le résultat du PGCD.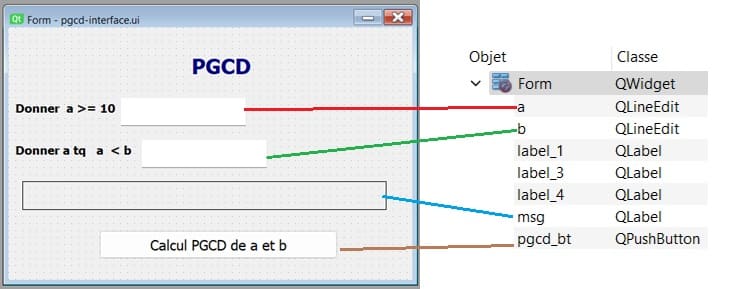
.ui, par exemple pgcd-interface.ui.2- Créer le script Python pour l'application
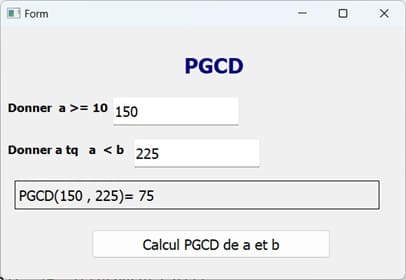
1) des exercices sur les chaînes des caractères
2) des exercices sur les tableaux
3) des sujets Bac pratique
4) des sujets Bac théorique
0 commentaire
laisser un commentaire
Tutoriels récents
Tutoriels populaires

Tutoriels plus commentés