Nombre K-parfait – Bac Pratique 2015 [ Algorithme + Python ]

Sujet bac informatique pratique 2015 (Bac scientifique)
Un nombre P est appelé k-parfait si et seulement si la somme de tous les diviseurs positifs de P, y compris 1 et lui-même, est égale à k*P. Avec k un entier naturel donnée.
Exemple :
28 est 2-parfait, car la somme de ses diviseurs est 56=2*28
120 est 3-parfait, car la somme de ses diviseurs est 360=3*120 ;
Ecrire un programme Python qui permet de chercher et d’afficher tous les nombres de l’intervalle [N, M] avec 10 < N ≤ M < 31000 qui sont 2-parfaits suivis par ceux qui sont 3-parfaits sur une autre ligne et ceux qui sont 4-parfaits sur une autre ligne.
Solution Algorithmique
Algorithme pour calculer les diviseurs d’un nombre :
Pour chaque nombre P de l'intervalle [N, M] :
1. Trouver tous les diviseurs de P en divisant P par les nombres compris entre 1 et p div 2 (seule la première moitié des diviseurs est calculée, et la seconde moitié est obtenue en prenant P / diviseur).
2. Calculer la somme de tous ces diviseurs, y compris P lui-même.
Vérification de la condition de k-parfait :
Pour chaque nombre P :
a) Si la somme des diviseurs est égale à 2 * P, ajouter P à la liste des nombres 2-parfaits.
b) Si la somme des diviseurs est égale à 3 * P, ajouter P à la liste des nombres 3-parfaits.
c) Si la somme des diviseurs est égale à 4 * P, ajouter P à la liste des nombres 4-parfaits.
Affichage des résultats :
Après avoir parcouru tous les nombres dans l'intervalle, afficher :
Les nombres 2-parfaits.
Les nombres 3-parfaits.
Les nombres 4-parfaits.
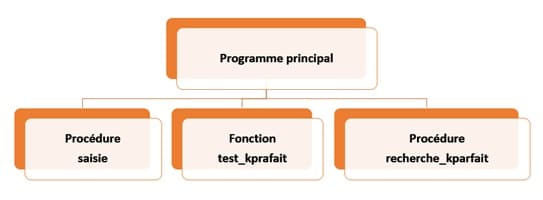
Dans cet algorithme, On va utiliser deux fonctions et une procédure:
Algorithme du programme principal
|
1 2 3 4 5 |
Algorithme nombre_kparfait Debut saisie() recherche_kparfait(n,m) Fin |
Déclaration des objets
|
Objet |
Type / Nature |
|
i |
entier |
|
n |
entier |
|
m |
entier |
La procédure saisie
Cette procédure saisit deux entiers m et n tel que 100≤n
Déclaration des objets Objet Type / Nature n entier m entier La fonction test_kparfait Cette fonction vérifie la condition de k-parfait pour un entier donné Déclaration des objets La procédure recherche_kparfait Cette procédure parcourt tous les nombres dans l'intervalle [n,m] et affiche : Les nombres 2-parfaits. Les nombres 3-parfaits. Les nombres 4-parfaits. Déclaration des objets Exécution du programme Pour créer une application en Python pour afficher tous les nombres k_parfait dans un intervalle [n,m] où 10≤n a- Ouvrez Qt Designer et créez un nouveau fichier de type Main Window. b- Ajoutez ces widgets: Enregistrez le fichier avec l'extension Voici un exemple de script Python qui utilise l'interface graphique générée par Qt Designer. Exécution du programme Vous pouvez voir aussi :
Objet
Type / Nature
i
entier
k
entier
Objet
Type / Nature
i
entier
k
entier
Solution en Python

Solution en Python et Designer QT
1- Créer l'interface graphique avec Qt Designer
QLineEdit nommé 'n' pour entrer un entier entre 10 et 31000.QLineEdit nommé 'm' pour entrer un entier m tq n=QLabel nommé 'msg' pour afficher un message d'erreur.QLabel nommé 'resultat' pour afficher les nombres kparfait.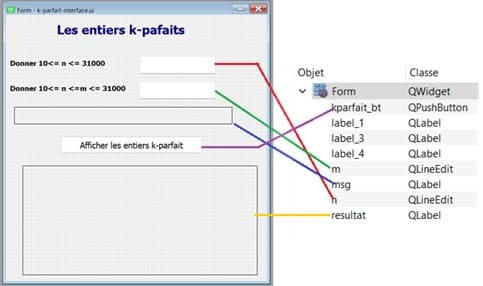
.ui, par exemple parfait-interface.ui.2- Créer le script Python pour l'application
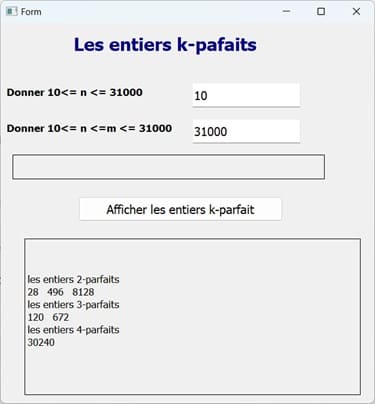
1) des exercices sur les chaînes des caractères
2) des exercices sur les tableaux
3) des sujets Bac pratique
4) des sujets Bac théorique
0 commentaire
laisser un commentaire
Tutoriels récents
Tutoriels populaires

Tutoriels plus commentés