Divisible par 7 – Bac Pratique 2015 [ Algorithme + Python ]

Sujet bac informatique pratique 2015 (Bac scientifique)
On se propose de construire à partir d’un chiffre E impaire donné une pyramide composée de L lignes. Chaque ligne est calculée en fonction de la ligne qui la précède en insérant à son début et à sa fin un chiffre C tel que:
C= (somme des chiffres de la ligne précédente+nombre de chiffres de la ligne précédente) Mod 10

Pour déterminer si un nombre N est divisible par 7, il suffit de le décomposer en des tranches de trois chiffres en commençant par la droite et d’insérer alternativement des + et des –devant les tranches en commençant par l’opérateur +. On effectue l’opération ainsi écrite, si le résultat est divisible par 7 alors n est divisble par 7.
Exemple : pour n=682068212860286 et en appliquant la règle de divisibilité par 7 ci-dessus, on obtient 286-860+212-068+682=252 qui est divisible par 7 donc n est divisible par 7.
Ecrire un programme Python qui permet de saisir un entier E impair (1≤E≤9), d’afficher les entiers correspondants à E selon le principe décrit précédemment à raison d’un entier par ligne. (Le candidat n’est pas appelé à afficher les entiers sous la forme d’une pyramide).
Solution Algorithmique
Pour résoudre ce problème, nous devons créer un algorithme qui, à partir d'un entier impair EE compris entre 1 et 9, génère plusieurs lignes d'entiers en fonction de la ligne précédente. Le nombre de lignes LL est défini par l'utilisateur.
1. Initialisation :
Demander à l'utilisateur de saisir un entier impair E tel que 1≤E≤9.
Demander à l'utilisateur de saisir le nombre de lignes L de la pyramide à générer.
2- Première ligne :
La première ligne de la pyramide est simplement l'entier E.
3- Génération des lignes suivantes :
Pour chaque nouvelle ligne, nous devons calculer un nouveau chiffre CC qui sera ajouté au début et à la fin de la ligne précédente.
La règle pour calculer C est : C=(somme des chiffres de la ligne précédente+ nombre de chiffres de la ligne précédente)mod 10
C = (somme des chiffres de la ligne précédente+ nombre de chiffres de la ligne précédente) mod 10
La nouvelle ligne sera construite en ajoutant ce chiffre C à la fois au début et à la fin de la ligne précédente.
La génération de la ligne s'arrête si l'entier généré est divisible par 7 selon le principe décrit au dessus.
4- Affichage :
À chaque itération, afficher la nouvelle ligne.
Dans cet algorithme, On va utiliser deux fonctions et une procédure :
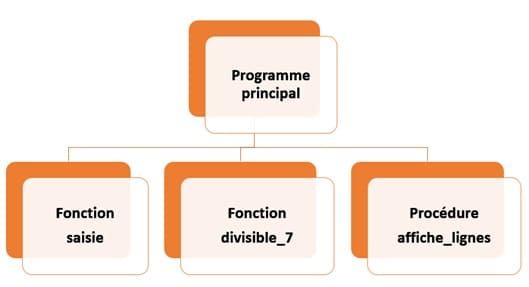
Algorithme du programme principal
|
1 2 3 4 5 |
Algorithme programme_afficher_lignes Debut e<-saisie() affiche_lignes(e) Fin |
La fonction saisie
Cette fonction retourne un chiffre impair.
|
1 2 3 4 5 6 7 8 9 10 |
Procedure saisie(): Début Ecrire('donner un entier impair entre 1 et 9:') lire (n) Tant que n<1 ou n>9 ou n mod 2 == 0 faire Ecrire('donner un entier impair entre 1 et 9:') lire (n) Fin tant que retourner n Fin |
Déclaration des objets
| Objet | Type / Nature |
|---|---|
| n | entier |
La fonction divisible_7
Cette fonction teste si un entier est divisible par 7
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 |
Fonction divisible_7(ch:chaine):booleen Début s<-0 ch1<-'' j<-0 # couper la chaine en tranches de 3 chiffres Pour i de 0 long(ch)-1 faire ch1<-ch[i]+ch1 Si ((i+1) mod 3 = 0) alors n<-Valeur(ch1) t[j]<-n ch1<-'' j<-j+1 Finsi Fin pour # Ajout la partie de la chaine qui reste Si ((ch1)!='') alors n<-Valeur(ch1) t[j]<-n j<-j+1 Fin si # Inserer alternativement des + et des – devant les tranches en commençant par l'operateur + Pour i de j-1 à -1 (pas=-1) faire Si (i mod 2 = 0): s<-s+t[i] Sinon s<-s-t[i] Fin pour # tester la divisibilité de s par 7 Si (s % 7=0) alors retourner Vrai Sinon retourner Faux Fin si Fin |
Déclaration des objets
| Objet | Type / Nature |
|---|---|
| i | entier |
| ch1 | chaîne des caractères |
| j | entier |
| t | tableau de 100 entiers |
| s | entier |
La procédure affiche_lignes
Cette procédure génère et affiche des lignes contenant des chiffres.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 |
Procédure affiche_lignes(e:entier) Début ch<-Convch(e) Ecrire(ch) Tant que (divisible_7(ch)=Faux) faire s<-0 Pour i de 0 à long(ch)-1 faire n<-Valeur(ch[i]) s<-s+n Fin pour s<-(s+long(ch)) mod 10 c<-Convch(s) ch<-c+ch+c Ecrire(ch) Fin |
Déclaration des objets
| Objet | Type / Nature |
|---|---|
| ch | chaîne des caractères |
| i | entier |
| c | caractère |
| s | entier |
Solution en Python
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 |
from numpy import array t=array([int()]*100) #declaration du tableau des entiers def saisie() : n=int(input("donner un entier impair entre 1 et 9: ")) while(n<1) or (n>9) or (n % 2 ==0) : n=int(input("donner un entier impair entre 1 et 9: ")) return n def divisible_7(ch): s=0 ch1='' j=0 # couper la chaine en tranches de 3 chiffres for i in range(len(ch)): ch1=ch[i]+ch1 if ((i+1) % 3 == 0): n=int(ch1) t[j]=n ch1='' j=j+1 # Ajout la partie de la chaine qui reste if ((ch1)!=''): n=int(ch1) t[j]=n j=j+1 # Inserer alternativement des + et des – devant les tranches en commençant par l'operateur + for i in range(j-1,-1,-1): if (i % 2 == 0): s=s+t[i] else: s=s-t[i] # tester la divisibilité de s par 7 if (s % 7==0): return True else: return False def affiche_lignes(e): ch=str(e) print(ch) while (divisible_7(ch)==False): s=0 for i in range(len(ch)): n=int(ch[i]) s=s+n s=(s+len(ch)) % 10 c=str(s) ch=c+ch+c print(ch) #programme principal e=saisie() affiche_lignes(e) |
Exécution du programme
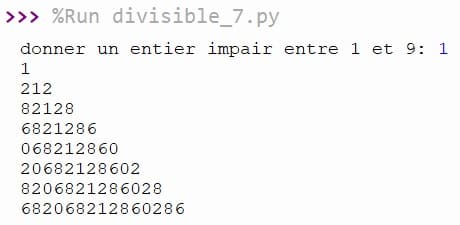
Solution en Python et Designer QT
Pour créer une application en Python pour construire à partir d’un chiffre E impaire donné une pyramide composée de L lignes en utilisant Qt Designer pour l'interface graphique, suivez ces étapes :
1- Créer l'interface graphique avec Qt Designer
a- Ouvrez Qt Designer et créez un nouveau fichier de type Main Window.
b- Ajoutez ces widgets:
QPushButton nommé 'afficher_bt' pour exécuter le module affiche_lignes().
QLabel nommé 'msg' pour afficher un message d'erreur et le résultat de la devinette du numéro de téléphone.
QLabel nommé 'resultat' pour afficher les lignes formées par des chiffres.
QLineEdit nommé 'e' pour entrer un chiffre impair.
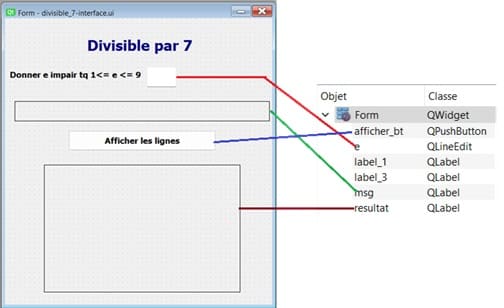
Enregistrez le fichier avec l'extension .ui, par exemple divisible_7-interface.ui.
2- Créer le script Python pour l'application
Voici un exemple de script Python qui utilise l'interface graphique générée par Qt Designer.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 |
from PyQt5.uic import loadUi from PyQt5 import QtCore, QtGui from PyQt5.QtWidgets import * from PyQt5 import QtCore, QtGui, QtWidgets app = QApplication([]) windows = loadUi ("divisible_7-interface.ui") from numpy import array t=array([int()]*100) #declaration du tableau des entiers def divisible_7(ch): s=0 ch1='' j=0 # couper la chaine en tranches de 3 chiffres for i in range(len(ch)): ch1=ch[i]+ch1 if ((i+1) % 3 == 0): n=int(ch1) t[j]=n ch1='' j=j+1 # Ajout la partie de la chaine qui reste if ((ch1)!=''): n=int(ch1) t[j]=n j=j+1 # Inserer alternativement des + et des – devant les tranches en commençant par l'operateur + for i in range(j-1,-1,-1): if (i % 2 == 0): s=s+t[i] else: s=s-t[i] # tester la divisibilité de s par 7 if (s % 7==0): return True else: return False def affiche_lignes(): windows.msg.clear() windows.resultat.clear() e = int(windows.e.text()) if 1<=e<=9 and e % 2 !=0 : ch=str(e) print(ch) liste=ch+'\n' while (divisible_7(ch)==False): s=0 for i in range(len(ch)): n=int(ch[i]) s=s+n s=(s+len(ch)) % 10 c=str(s) ch=c+ch+c liste=liste+ch+'\n' print(ch) windows.resultat.setText(liste) else: windows.msg.setText('Veuillez saisir un seul chiffre impair') windows.afficher_bt.clicked.connect(affiche_lignes) windows.show() app.exec_() |
Exécution du programme
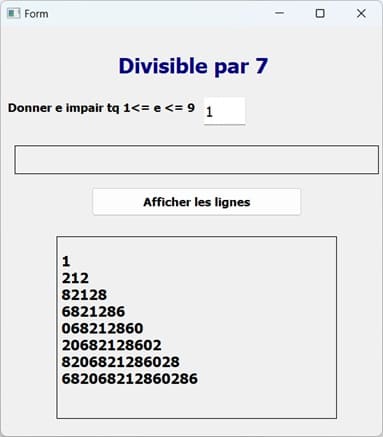
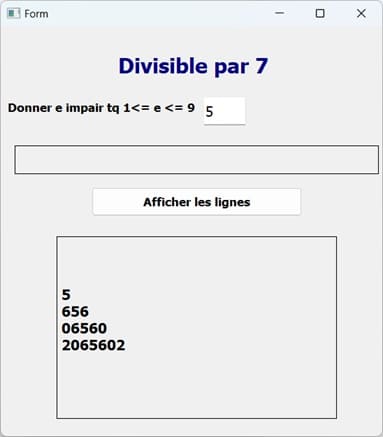
Vous pouvez voir aussi :
1) des exercices sur les chaînes des caractères
2) des exercices sur les tableaux
3) des sujets Bac pratique
4) des sujets Bac théorique
0 commentaire
laisser un commentaire
Tutoriels récents
Tutoriels populaires

Tutoriels plus commentés