Divisibilité par 7 – Examen pratique informatique – 2024 [Bac scientifique]

Sujet bac informatique pratique 2024 (Bac scientifique)
On se propose d'écrire un algorithme et un programme Python permettant de saisir un nombre X formé de 5 à 20 chiffres, puis de vérifier s’il est divisible par 7 en utilisant le principe suivant :
Etape1 : Former, à partir du nombre X, un nouveau nombre Y en faisant correspondre à chaque chiffre de X le reste de sa division euclidienne par 7.
Exemple

Etape2 : Former, à partir du nombre Y, un nouveau nombre Z en faisant correspondre à chaque tranche de deux chiffres de Y (en commençant à partir de la droite), le reste de sa division euclidienne par 7.
Exemple
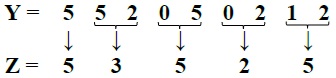
- En effet, pour la tranche 12 de Y, lui correspond dans Z la valeur 5 (reste de la division euclidienne de 12 par 7).
- De même pour les autres tranches.
- La dernière tranche se compose d’un seul chiffre car le nombre de chiffres de Y est impair.
Etape3 : Appliquer au nombre Z, la méthode de Horner définie par l’algorithme suivant de la fonction Horner(Z).
|
1 2 3 4 5 6 7 8 9 10 |
Fonction Horner(Z : Chaîne de caractères) : Entier DEBUT M <- 0 Tant que Z <> "" Faire CH <- Z[0] M <- (M * 2 + Valeur(CH)) Mod 7 Z <- Sous_chaine(Z, 1, Long(Z)) Fin Tant que Retourner M FIN |
Déclaration des objets
| Objet | Type / Nature |
|---|---|
| M | entier |
| CH | chaîne des caractères |
Le nombre X est divisible par 7 lorsque la fonction Horner, appliquée au nombre Z, retourne la valeur zéro.
Solution Algorithmique
Dans cet algorithme, On va utiliser trois fonctions et deux procédures:
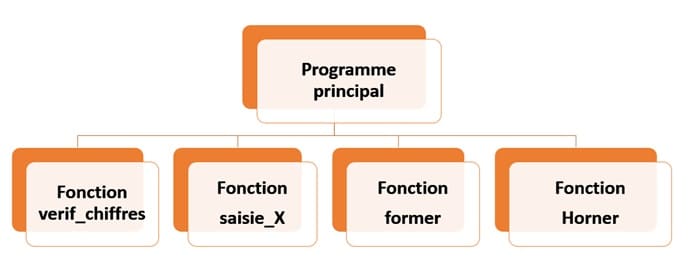
Algorithme du programme Principal
|
1 2 3 4 5 6 7 8 9 |
Algorithme divisible_7 Debut x<-saisie_X() Si (Horner(former(x))) alors Ecrire(x+' est divisible par 7 ') Sinon Ecrire(x+' est non divisible par 7 ') Finsi Fin |
Déclaration des objets
| Objet | Type / Nature |
|---|---|
| x | entier |
La fonction verif_chiffres
Cette fonction vérifie que 'une chaîne donnée est formés de 5 à 20 chiffres.
|
1 2 3 4 5 6 7 8 9 10 11 12 |
fonction verif_chiffres(ch:chaine):booleen Début Si 5<=long(ch)<=20 alors i<-0 Tant que (i<long(ch)-1) et ('0'<=ch[i]<='9') faire i<-i+1 Fin tant que retourner (('0'<=ch[i]<='9')) Sinon retourner Faux Fin si Fin |
Déclaration des objets
| Objet | Type / Nature |
|---|---|
| i | entier |
La fonction saisie_X
Cette fonction saisit une chaine formée de 5 à 20 chiffres
|
1 2 3 4 5 6 7 8 9 10 |
fonction saisie_X():chaine Début Ecrire("donner un nombre forme de 5 a 20 chiffres: ") Lire(ch) Tant que (verif_chiffres(ch)=Faux) faire Ecrire("donner un nombre forme de 5 a 20 chiffres : ") Lire(ch) Fin tant que retourner ch Fin |
Déclaration des objets
| Objet | Type / Nature |
|---|---|
| ch | chaîne des caractères |
La fonction former
Cette fonction forme à partir du nombre X, un nouveau nombre Y en faisant correspondre à chaque chiffre de X le reste de sa division euclidienne par 7.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 |
fonction former(x:chaine):chaine Début y<-'' Pour i de 0 à long(x)-1 faire y<-y+Convch(Valeur(x[i])%7) Fin pour z<-'' Si (long(y) mod 2=0) alors # si la nombre des chiffres est paire Pour i de 0 à ((long(y) div 2) -1) faire z<-z+(Convch(Valeur(y[i*2]+y[i*2+1]) mod 7)) Sinon # si la nombre des chiffres est impaire z<-z+Convch(Valeur(y[0]) mod 7) Pour i de 1 à (long(y) div 2)) faire z<-z+(Convch(Valeur(y[i*2-1]+y[i*2]) mod 7)) Fin pour Finsi retourner z Fin |
Déclaration des objets
| Objet | Type / Nature |
|---|---|
| i | entier |
| y | entier |
| z | entier |
La fonction Horner
Cette fonction applique au nombre Z, la méthode de Horner et retourne le résultat.
Appliquer au nombre Z, la méthode de Horner définie par l’algorithme suivant de la fonction Horner(Z).
|
1 2 3 4 5 6 7 8 9 10 |
Fonction Horner(Z : Chaîne de caractères) : Entier DEBUT M <- 0 Tant que Z <> "" Faire CH <- Z[0] M <- (M * 2 + Valeur(CH)) Mod 7 Z <- Sous_chaine(Z, 1, Long(Z)) Fin Tant que Retourner M FIN |
Déclaration des objets
| Objet | Type / Nature |
|---|---|
| M | entier |
| CH | chaîne des caractères |
Solution en Python
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 |
def verif_chiffres(ch) : if 5<=len(ch)<=20 : i=0 while (i<len(ch)-1) and ('0'<=ch[i]<='9'): i=i+1 return (('0'<=ch[i]<='9')) else: return False def saisie_X(): ch=input("donner un nombre forme de 5 a 20 : ") while (verif_chiffres(ch)==False) : ch=input("donner un nombre forme de 5 a 20 : ") return ch def former(x): y='' for i in range(len(x)): y=y+str(int(x[i])%7) z='' if (len(y)%2==0): for i in range(len(y)//2): z=z+(str(int(y[i*2]+y[i*2+1])%7)) else: z=z+str(int(y[0])%7) for i in range(1,(len(y)//2)+1): z=z+(str(int(y[i*2-1]+y[i*2])%7)) return z def Horner(z): m=0 while (z!='') : ch=z[0] m=(m*2+int(ch))%7 z=z[1:len(z)] if m==0 : return True else: return False x=saisie_X() if(Horner(former(x))): print(x+' est divisible par 7 ') else: print(x+' est non divisible par 7 ') |
Exécution du programme:

Solution en Python et Designer QT
Pour créer une application en Python et Designer QT qui vérifie si un nombre est divisible par 7 selon le principe décrit ci-dessus, on va suivre ces étapes:
1- Créer l'interface graphique avec Qt Designer
a- Ouvrez Qt Designer et créez un nouveau fichier de type Main Window.
b- Ajoutez ces widgets:
QLineEdit nommé 'x' pour entrer un nombre
QLabel nommé 'msg' pour contenir les messages d'erreur et le résultat de la divisibilité du nombre par 7.
QPushButton nommé 'verifier_bt' pour vérifier si le nombre est divisible par 7.
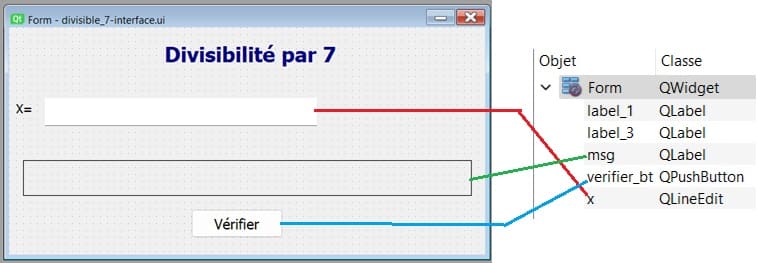
Enregistrez le fichier avec l'extension .ui, par exemple divisible_7-interface.ui.
2- Créer le script Python pour l'application
Voici un exemple de script Python qui utilise l'interface graphique générée par Qt Designer.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 |
from PyQt5.uic import loadUi from PyQt5.QtWidgets import QApplication app = QApplication([]) windows = loadUi ("divisible_7-interface.ui") def verif_chiffres(ch) : if 5<=len(ch)<=20 : i=0 while (i<len(ch)-1) and ('0'<=ch[i]<='9'): i=i+1 return (('0'<=ch[i]<='9')) else: return False def former(x): y='' for i in range(len(x)): y=y+str(int(x[i])%7) z='' if (len(y)%2==0): for i in range(len(y)//2): z=z+(str(int(y[i*2]+y[i*2+1])%7)) else: z=z+str(int(y[0])%7) for i in range(1,(len(y)//2)+1): z=z+(str(int(y[i*2-1]+y[i*2])%7)) return z def play(): windows.msg.clear() x = windows.x.text() if verif_chiffres(x): z=former(x) m=0 while (z!='') : ch=z[0] m=(m*2+int(ch))%7 z=z[1:len(z)] if m==0 : windows.msg.setText(x+' est divisible par 7 ') else: windows.msg.setText(x+" n'est pas divisible par 7 ") else: windows.msg.setText("Veuillez saisir un nombre de 5 a 20 chiffres") windows.verifier_bt.clicked.connect(play) windows.show() app.exec_() |
Exécution du programme
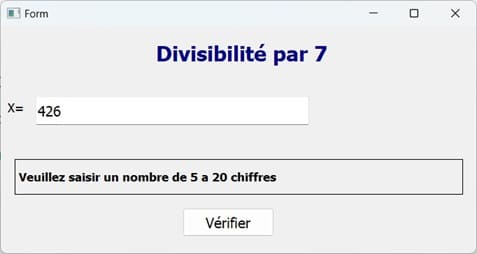
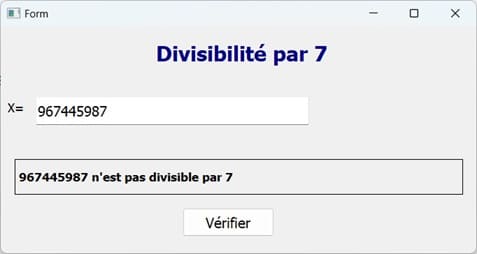
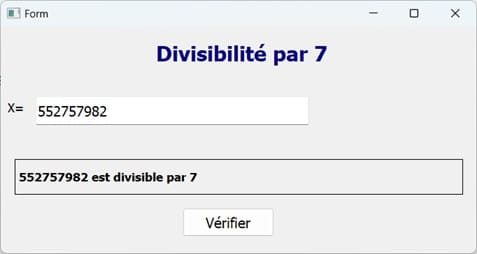
Vous pouvez voir aussi :
1) des exercices sur les chaînes des caractères
2) des exercices sur les tableaux
3) des sujets Bac pratique
4) des sujets Bac théorique
0 commentaire
laisser un commentaire
Tutoriels récents
Tutoriels populaires

Tutoriels plus commentés