Suite arithmétique – Examen pratique informatique – 2024 [Bac scientifique]

Sujet bac informatique pratique 2024 (Bac scientifique)
On se propose d'écrire un algorithme et un programme Python permettant de saisir un nombre X, de longueur paire et composé de 6 à 20 chiffres, puis de vérifier si toutes les tranches successives de deux chiffres de X, une fois triées dans l’ordre croissant, constituent des termes d’une suite arithmétique croissante.
Une suite arithmétique croissante est une suite dans laquelle chaque terme permet de déduire le suivant en lui ajoutant une constante r appelée raison (pour tout n > 0 ; Un = Un-1 + r avec r > 0).
Exemples :
Pour X = 301015250520 ;
Les tranches de X :
![]()
Les tranches de X triées :
![]()
Les tranches successives de X, une fois triées dans l’ordre croissant, forment des termes d’une suite arithmétique croissante de raison r = 5. En effet, (10 – 5) = (15 – 10) = (20 – 15) = (25 – 20) = (30 – 25) = 5
Pour X = 41331020 ;
Les tranches de X :
![]()
Les tranches de X triées :
![]()
Les tranches successives de X, une fois triées dans l’ordre croissant, ne forment pas des termes d’une suite arithmétique croissante.
Solution Algorithmique
Dans cet algorithme, On va utiliser trois fonctions et une procédure:
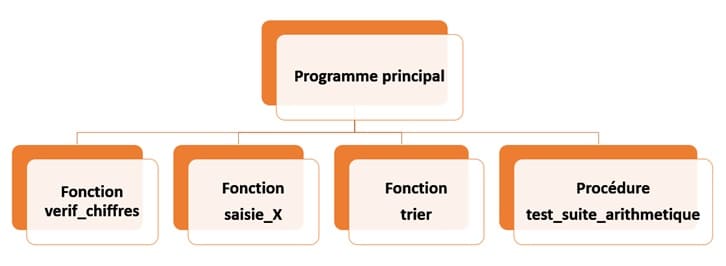
Algorithme du programme Principal
|
1 2 3 4 5 6 7 |
Algorithme suite_arithmetique Debut x<-saisie_X() x<-trier(x) Ecrire("Les tranches des chiffres triees "+x) test_suite_arithmetique(x) Fin |
Déclaration des objets
| Objet | Type / Nature |
|---|---|
| x | chaîne des caractères |
La fonction verif_chiffres
Cette fonction vérifie qu'une chaine est de longueur paire et composé de 6 à 20 chiffres.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 |
fonction verif_chiffres(ch:chaine):booleen Début #verifie qu'une chaine est de longueur paire et sa longueur entre de 6 et 20 Si 6<=long(ch)<=20 et long(ch) mod 2=0 alors i<-0 # verifier que la chaine est composee des chiffres. Tant que (i<long(ch)-1) et ('0'<=ch[i]<='9') faire i<-i+1 Fin tant que retourner (('0'<=ch[i]<='9')) Sinon retourner Faux Fin si Fin |
Déclaration des objets
| Objet | Type / Nature |
|---|---|
| i | entier |
La fonction saisie_X
Cette fonction saisit une chaine est de longueur paire et composé de 6 à 20 chiffres.
|
1 2 3 4 5 6 7 8 9 10 |
fonction saisie_X():chaine Début Ecrire("donner un nombre forme de 6 a 20 chiffres pairs: ") Lire(ch) Tant que (verif_chiffres(ch)=Faux) faire Ecrire("donner un nombre forme de 6 a 20 chiffres pairs: ") Lire(ch) Fin tant que retourner ch Fin |
Déclaration des objets
| Objet | Type / Nature |
|---|---|
| ch | chaîne des caractères |
La procédure trier
Cette procédure permet de trier dans l’ordre croissant les tranches de deux chiffres de la chaîne CH.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 |
Fonction Trier(CH : Chaîne de caractères) : Chaîne de caractères DEBUT PERMUT <- Vrai Tant que PERMUT Faire PERMUT <- Faux Pour K de 0 à Long(CH)-3) [Pas=2] Faire BLOC1<- Sous_chaîne(CH, K, K+2) BLOC2<- Sous_chaîne(CH, K+2, K+4) Si BLOC1>BLOC2 Alors CH<- Sous_chaîne(CH, 0, K)+BLOC2+BLOC1+Sous_chaîne(CH, K+4, Long(CH)) PERMUT <- Vrai FinSi Fin Pour Fin Tant que Retourner CH FIN |
Déclaration des objets
| Objet | Type / Nature |
|---|---|
| K | entier |
| PERMUT | booleen |
| BLOCK1 | chaîne des caractères |
| BLOCK2 | chaîne des caractères |
La procédure test_suite_arithmetique
Cette procédure vérifie si les chiffres qui constitue un nombre forme une suite arithmétique croissante.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 |
Procedure test_suite_arithmetique(ch:chaine) DEBUT # calculer la raison de la suite r<-Valeur(Sous_chaine(ch,2,4))-valeur(Sous_chaine(ch,0,2)) i<-0 # verifier que la raison de la suite est constante Tant que (i<long(ch)-2) et (Valeur(Sous_chaine(ch,i+2,i+4))-Valeur(Sous_chaine(ch,i,i+2))=r) alors i<-i+2 Fin tant que Si i=long(ch)-2 alors Ecrire("forment une des termes d'une suite arithmetique (r="+r+")") Sinon Ecrire("ne forment pas une des termes d'une suite arithmetique") Finsi FIN |
Déclaration des objets
| Objet | Type / Nature |
|---|---|
| i | entier |
| r | entier |
Solution en Python
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 |
def verif_chiffres(ch) : if 6<=len(ch)<=20 and len(ch)%2==0: i=0 while (i<len(ch)-1) and ('0'<=ch[i]<='9'): i=i+1 return (('0'<=ch[i]<='9')) else: return False def saisie_X(): ch=input("donner un nombre forme de 6 a 20 chiffres pairs: ") while (verif_chiffres(ch)==False) : ch=input("donner un nombre forme de 5 a 20 chiffres pairs: ") return ch def trier(CH) : PERMUT=True while PERMUT : PERMUT=False for K in range(0, len(CH)-3, 2) : BLOC1=CH[K:K+2] BLOC2=CH[K+2:K+4] if BLOC1>BLOC2 : CH=CH[0:K]+BLOC2+BLOC1+CH[K+4:len(CH)] PERMUT=True return CH def test_suite_arithmetique(ch): r=int(ch[2:4])-int(ch[0:2]) i=0 while (i<len(ch)-2) and (int(ch[i+2:i+4])-int(ch[i:i+2])==r) : i=i+2 if i==len(ch)-2 : print("forment une des termes d'une suite arithmetique (r="+str(r)+")") else: print("ne forment pas une des termes d'une suite arithmetique") #programme principal x=saisie_X() x=trier(x) print("Les tranches des chiffres triees "+x) test_suite_arithmetique(x) |
Exécution du programme:
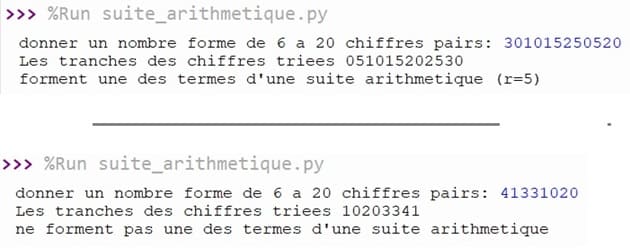
Solution en Python et Designer QT
Pour créer une application en Python et Designer QT qui de saisir un nombre X puis de vérifier si toutes les tranches successives de deux chiffres de X, une fois triées dans l’ordre croissant, constituent des termes d’une suite arithmétique croissante., on va suivre ces étapes:
1- Créer l'interface graphique avec Qt Designer
a- Ouvrez Qt Designer et créez un nouveau fichier de type Main Window.
b- Ajoutez ces widgets:
QLineEdit nommé 'x' pour entrer un nombre x
QLabel nommé 'msg' pour contenir les messages d'erreur et le résultat de la vérification du nombre.
QPushButton nommé 'verifier_bt' pour tester si les tranches successives de deux chiffres de X, une fois triées dans l’ordre croissant, constituent des termes d’une suite arithmétique croissante.
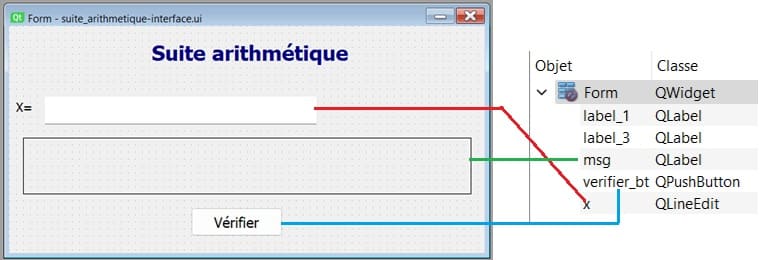
Enregistrez le fichier avec l'extension .ui, par exemple suite_arithmetique-interface.ui.
2- Créer le script Python pour l'application
Voici un exemple de script Python qui utilise l'interface graphique générée par Qt Designer.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 |
from PyQt5.uic import loadUi from PyQt5.QtWidgets import QApplication app = QApplication([]) windows = loadUi ("suite_arithmetique-interface.ui") def verif_chiffres(ch) : if (6<=len(ch)<=20) and (len(ch)%2==0): i=0 while (i<len(ch)-1) and ('0'<=ch[i]<='9'): i=i+1 return (('0'<=ch[i]<='9')) else: return False def trier(CH) : PERMUT=True while PERMUT : PERMUT=False for K in range(0, len(CH)-3, 2) : BLOC1=CH[K:K+2] BLOC2=CH[K+2:K+4] if BLOC1>BLOC2 : CH=CH[0:K]+BLOC2+BLOC1+CH[K+4:len(CH)] PERMUT=True return CH def play(): windows.msg.clear() x = windows.x.text() if verif_chiffres(x): ch=trier(x) resultat="Les tranches des chiffres triees "+ch+"\n" r=int(ch[2:4])-int(ch[0:2]) i=0 while (i<len(ch)-2) and (int(ch[i+2:i+4])-int(ch[i:i+2])==r) : i=i+2 if i==len(ch)-2 : resultat=resultat+"forment une des termes d'une suite arithmetique (r="+str(r)+")" else: resultat=resultat+"ne forment pas une des termes d'une suite arithmetique" windows.msg.setText(resultat) else: windows.msg.setText("Veuillez saisir un nombre de 6 a 20 chiffres et de longueur pair ") windows.verifier_bt.clicked.connect(play) windows.show() app.exec_() |
Exécution du programme
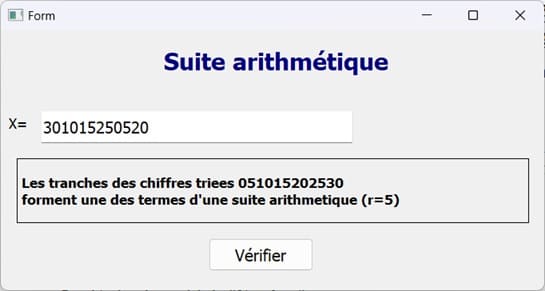
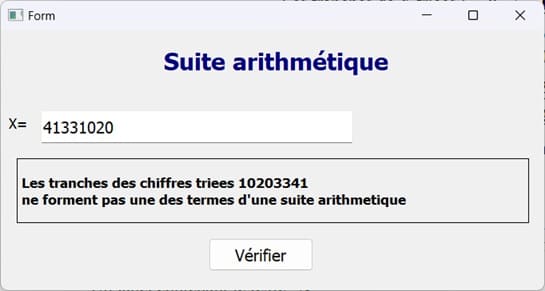
Vous pouvez voir aussi :
1) des exercices sur les chaînes des caractères
2) des exercices sur les tableaux
3) des sujets Bac pratique
4) des sujets Bac théorique
0 commentaire
laisser un commentaire
Tutoriels récents
Tutoriels populaires

Tutoriels plus commentés




















