Nombre semi-premier – Examen pratique informatique – 2022 [ Bac scientifique ]

Sujet bac informatique pratique 2022 (Bac scientifique)
Un nombre N est dit semi-premier lorsqu’il est égal au produit de deux nombres premiers non nécessairement distincts. C’est-à-dire N = k*k avec k est un nombre premier ou N = k*j avec k et j sont deux nombres premiers.
Exemples :
- 6 est un nombre semi-premier car 6 = 2 × 3 avec 2 et 3 sont deux nombres premiers.
- 25 est un nombre semi-premier car 25 = 5 × 5 avec 5 est un nombre premier.
- 831 est un nombre semi-premier car 831= 3 × 277 avec 3 et 277 sont deux nombres premiers
- 8 n’est pas un nombre semi-premier, car 8 = 2 × 4 avec 4 n’est pas un nombre premier.
Pour vérifier si un entier naturel N (N > 2) est un nombre semi-premier ou non, on propose un algorithme et un programme Python.
Solution Algorithmique
Dans cet algorithme, On va utiliser 3 fonctions :
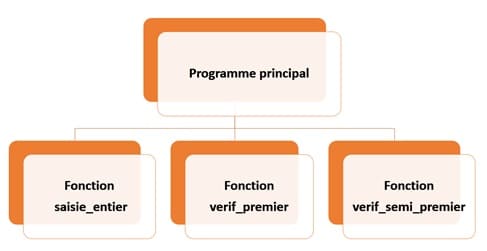
Algorithme du programme Principal
|
1 2 3 4 5 6 7 8 9 |
Algorithme nombre_semi-premier Debut n<-saisie_entier() Si verif_semi_premier(n) alors Ecrire(n+' est semi-premier') Sinon Ecrire(n+" n'est pas semi-premier") Fin si Fin |
Déclaration des objets
| Objet | Type / Nature |
|---|---|
| n | entier |
La fonction saisie_entier
Cette fonction saisit un entier > 2.
|
1 2 3 4 5 6 7 8 9 10 |
fonction saisie_entier():entier Début Ecrire("donner un entier >= 3) Lire(n) Tant que (n<3) faire Ecrire("donner un entier >= 3) Lire(n) Fin tant que retourner n Fin |
Déclaration des objets
| Objet | Type / Nature |
|---|---|
| n | entier |
La fonction verif_premier
Cette fonction vérifie si un entier est premier.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 |
fonction verif_premier(n:entier):booleen Début Si (n>2) alors i<-2 # recherche des diviseurs possibles Tant que (i<(n div 2)) et (n mod i!=0) alors i<-i+1 Fin tant que retourner (n mod i!=0) Sinon si n=2 alors return Vrai Fin si Fin |
Déclaration des objets
| Objet | Type / Nature |
|---|---|
| i | entier |
La fonction verif_semi_premier
Cette fonction vérifie si un nombre est semi-premier.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 |
fonction verif_semi_premier(n:entier):booleen Début Si verif_premier(n)=Faux alors i<-2 test_trouve<-Faux Tant que (i<(n div 2)+1) et (test_trouve=Faux) faire # recherche les diviseurs k et j tq n=k*j # verifier si ces diviseurs sont premiers Si ((n div i)=0) et (verif_premier(i) et verif_premier(n div i)) alors Ecrire(n+'='+i+'x'+ n div i) test_trouve<-Vrai Fin si i<-i+1 Fin tant que retourner test_trouve=Vrai Sinon retourner Faux Fin si Fin |
Déclaration des objets
| Objet | Type / Nature |
|---|---|
| i | entier |
| test_trouve | booleen |
Solution en Python
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 |
def saisie_entier(): n=int(input("donner un entier >2: ")) while (n<2): n=int(input("donner un entier >2: ")) return n def verif_premier(n): if (n>2): i=2 # recherche des diviseurs possibles while (i<(n//2)) and (n % i!=0): i=i+1 return (n % i!=0) elif n==2: return True def verif_semi_premier(n): if verif_premier(n)==False : i=2 test_trouve=False while (i<(n//2)+1) and (test_trouve==False): # recherche les diviseurs k et j tq n=k*j # verifier si ces diviseurs sont premiers if ((n % i)==0) and (verif_premier(i) and verif_premier(n//i)): print(str(n)+'='+str(i),'x', str(n//i)) test_trouve=True i=i+1 return test_trouve==True else: return False #programme principal n=saisie_entier() if verif_semi_premier(n) : print(str(n)+' est semi-premier') else: print(str(n)+" n'est pas semi-premier") |
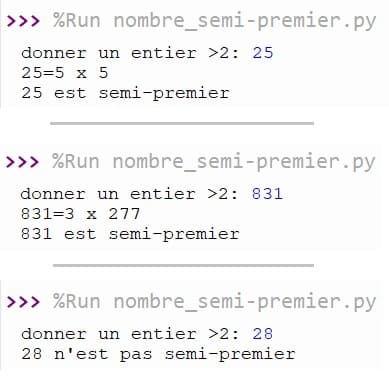
Exécution du programme:
Solution en Python et Designer QT
Pour créer une application en Python et Designer QT qui saisit un nombre >2 et vérifie s'il est semi-premier ou non , on va suivre ces étapes:
1- Créer l'interface graphique avec Qt Designer
a- Ouvrez Qt Designer et créez un nouveau fichier de type Main Window.
b- Ajoutez ces widgets:
QLineEdit nommé 'n' pour entrer un entier >2.
QPushButton nommé 'verifier_bt' pour vérifier si n est un nombre semi-premier
QLabel nommé 'msg' pour afficher des messages d'erreur et le résultat de la vérification du nombre.
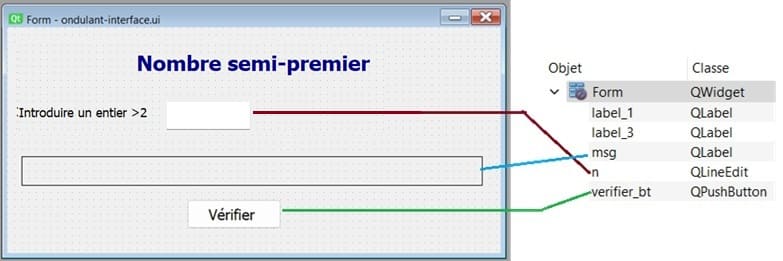
Enregistrez le fichier avec l'extension .ui, par exemple nombre_semi-premier-interface.ui.
2- Créer le script Python pour l'application
Voici un exemple de script Python qui utilise l'interface graphique générée par Qt Designer.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 |
from PyQt5.uic import loadUi from PyQt5.QtWidgets import QApplication app = QApplication([]) windows = loadUi ("nombre_semi-premier-interface.ui") def verif_premier(n): if (n>2): i=2 # recherche des diviseurs possibles while (i<(n//2)) and (n % i!=0): i=i+1 return (n % i!=0) elif n==2: return True def play(): windows.msg.clear() n = int(windows.n.text()) if n > 2 : if verif_premier(n)==False : i=2 test_trouve=False resultat_test='' while (i<(n//2)+1) and (test_trouve==False): # recherche les diviseurs k et j tq n=k*j # verifier si ces diviseurs sont premiers if ((n % i)==0) and (verif_premier(i) and verif_premier(n//i)): resultat_test=str(n)+'='+str(i)+'x'+ str(n//i)+'\n' test_trouve=True i=i+1 if test_trouve : resultat_test=resultat_test+str(n)+' est semi-premier' else: resultat_test=str(n)+" n'est pas semi-premier" else: resultat_test=str(n)+" n'est pas semi-premier" windows.msg.setText(resultat_test) else: windows.msg.setText(" Veuillez introduire un nombre > 2 ") windows.verifier_bt.clicked.connect(play) windows.show() app.exec_() |
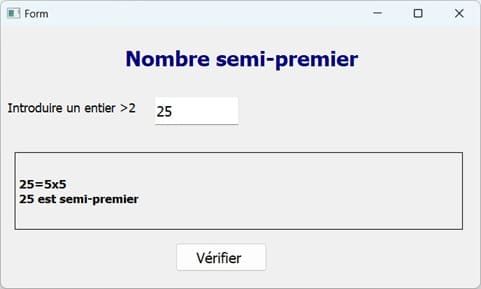
Exécution du programme
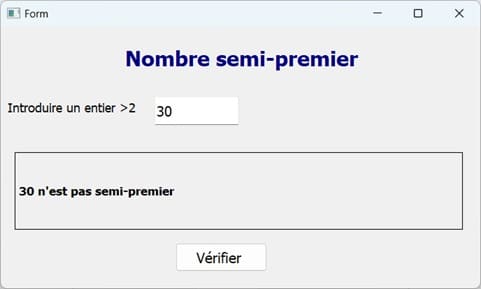
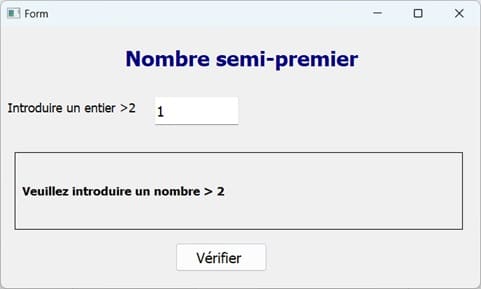
Vous pouvez voir aussi :
1) des exercices sur les chaînes des caractères
2) des exercices sur les tableaux
3) des sujets Bac pratique
4) des sujets Bac théorique
0 commentaire
laisser un commentaire
Tutoriels récents
Tutoriels populaires

Tutoriels plus commentés