Bac scientifique Théorique 2012 [ Algorithme + Python ]

Travail demandé
On se propose d’écrire un programme qui saisit un entier naturel n (2 <= n<=20), puis remplit un tableau T1 par N nombres complexes de la forme a+bi avec a et b deux entiers naturels non nuls. Chaque suite d’éléments du tableau T1 qui ont le même module sera affiché sur une ligne à part. On rappelle que le module d’un nombre complexe de la forme a+bi est racine carré (a²+b²)
Pour réaliser le traitement demandé on suivra les étapes suivantes :
1- Remplir un tableau T2 par les modules des éléments de T1 de façon à ce que T2[i] soit le module du nombre complexe T[i].
2- Trier simultanément les deux tableaux T1 et T2 selon l’ordre décroissant des valeurs du tableau T2
3- Afficher chaque suite d’éléments du tableau T qui ont le même module sur une ligne à part.
Exemple : Pour n=6 et pour le tableau T2 suivant :
| 2+3i | 2+15i | 2+17i | 23+3i | 17+2i | 15+2i |
Le remplissage de T2 donne le tableau suivant :
| 3.60 | 15.13 | 17.12 | 23.19 | 17.12 | 15.13 |
Après le tri on obtient les deux tableaux suivants :
T1 T :
| 23+3i | 2+17i | 17+2i | 2+15i | 15+2i | 2+3i |
T2 :
| 23.19 | 17.12 | 17.12 | 15.13 | 15.13 | 3.60 |
Le programme affiche les lignes suivantes :
23+3i
2+17i 17+2i
2+15i 15+2i
2+3i
Solution Algorithmique
Pour résoudre ce problème, nous allons suivre les étapes mentionnées. Le programme commencera par saisir un nombre n (2 ≤ n ≤ 20), puis remplira un tableau T1 avec des nombres complexes sous la forme a+bi. Ensuite, il calculera les modules de ces nombres complexes et les stockera dans un tableau T2. Enfin, il triera simultanément les tableaux T1 et T2 selon l'ordre décroissant des modules et affichera les nombres complexes ayant le même module sur des lignes séparées.
Détails des étapes :
1- Saisie et initialisation : On demande à l'utilisateur de saisir n et les parties réelles et imaginaires des nombres complexes.
2- Calcul des modules : Pour chaque nombre complexe a+bi, on calcule le module en utilisant la formule racine carré (a²+b²) et on stocke ce module dans T2.
3- Tri simultané des tableaux : Les deux tableaux T1 et T2 sont triés selon les valeurs décroissantes de T2 en utilisant l'algorithme tri à bulles.
4- Affichage : On parcourt les tableaux triés et on affiche les nombres complexes du tableau T1 en les regroupant par modules similaires.
Dans cet algorithme, On va utiliser deux fonctions et deux procédures:
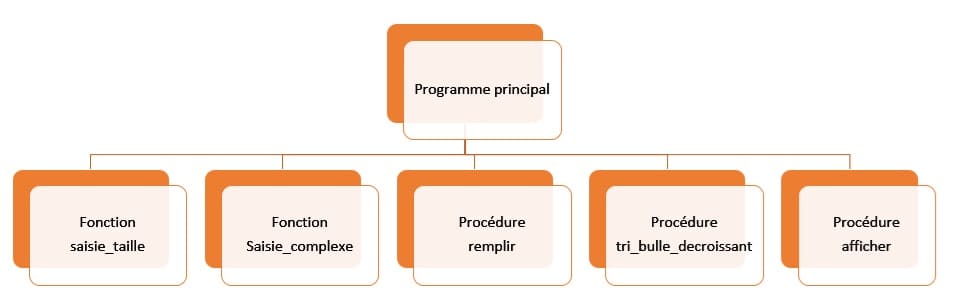
Algorithme du programme principal
|
1 2 3 4 5 6 7 8 9 10 |
Algorithme super Debut n<-saisie() Ecrire('remplissage des tableaux t1 et t2') remplir(t1,t2,n) Ecrire('Trier les deux tableaux t1 et t2') tri_bulle_decroissant(t1,t2,n) Ecrire('affichage') afficher(t1,t2,n) Fin |
Déclaration des objets
Objet | Type / nature |
n | entier |
t1 | tableau des chaînes de caratctères |
t2 | tableau des réels |
La fonction saisie
Cette fonction retourne un entier n entre 1 et 30 saisi par l'utilisateur.
|
1 2 3 4 5 6 7 8 9 10 |
foncttion saisie_taille() Début Ecrire('donner un entier entre 1 et 30') lire (n) Tant que n<1 ou n>30 faire Ecrire('donner un entier entre 1 et 30') lire (n) Fin tant que retourner n Fin |
Déclaration des objets
Objet | Type / Nature |
n | entier |
La fonction saisie_complexe
Cette fonction saisit un nombre complexe .
|
1 2 3 4 5 6 7 8 9 10 |
Procédure saisie_complexe() Début Ecrire('donner un entier >0') lire (n) Tant que n<=0 faire Ecrire('donner un entier > 0') lire (n) Fin tant que retourner n Fin |
Déclaration des objets
Objet | Type / Nature |
n | entier |
La procédure remplir
Cette procédure remplit les deux tableau t1 et t2 de n entiers.
|
1 2 3 4 5 6 7 8 9 |
Procédure remplir(@t:Tab,n:entier) Début Pour i de 0 à n-1 faire a<-saisie_complexe() b<-saisie_complexe() t1[i]<-Convch(a)+'+'+Convch(b)+'i' t2[i]<-format(math.sqrt(a*a+b*b), '.2f') Fin pour Fin |
Déclaration des objets
Objet | Type / nature |
i | entier |
a | entier |
b | entier |
La procédure tri_bulle_decroissant
Cette procédure trie les deux tableaux T1 et T2 selon les valeurs décroissantes de T2 en utilisant l'algorithme tri à bulles.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 |
Procédure tri_bulle_decroissant(t1,t2,n) Début n1<-n permuter<-Vrai Tant que (permuter=Vrai) et ( n1>1) : permuter<-Faux Pour i de 0 à n-2 faire Si (t2[i]<t2[i+1]): permuter<-Vrai temp2<-t2[i] t2[i]<-t2[i+1] t2[i+1]<-temp2 temp1<-t1[i] t1[i]<-t1[i+1] t1[i+1]<-temp1 Fin pour n1<-n1-1 Fin tantque Fin |
Déclaration des objets
Objet | Type / Nature |
i | entier |
permuter | booléen |
temp1 | chaîne des cartectères |
temp2 | réel |
La procédure afficher
Cette procédure parcourt les tableaux triés et on affiche les nombres complexes du tableau T1 en les regroupant par modules similaires.
|
1 2 3 4 5 6 7 8 9 10 |
Procédure afficher(t1,t2,n) Début écrire(t1[0]) Pour i de 1 à n-1 faire Si t2[i-1]!=t2[i] alors retour à la ligne finsi écrire(t1[i]) Fin pour Fin |
Déclaration des objets
Objet | Type / Nature |
i | entier |
Solution en Python
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 |
from numpy import array import math t1=array([str]*30) t2=array([float()]*30) def saisie_taille() : n=int(input("donner un entier entre 1 et 30 ")) while(1>n) and(n>30) : n=int(input("donner un entier entre 1 et 30 ")) return n def saisie_complexe() : n=int(input("donner un entier >0 ")) while (n<=0) : n=int(input("donner un entier >0 ")) return n def remplir(t1,t2,n): for i in range (n) : a=saisie_complexe() b=saisie_complexe() t1[i]=str(a)+'+'+str(b)+'i' t2[i]=format(math.sqrt(a*a+b*b), '.2f') def tri_bulle_decroissant(t1,t2,n): n1=n permuter=True; while (permuter==True) and ( n1>1) : permuter=False for i in range (0,n1-1): if (t2[i]<t2[i+1]): permuter=True temp2=t2[i] t2[i]=t2[i+1] t2[i+1]=temp2 temp1=t1[i] t1[i]=t1[i+1] t1[i+1]=temp1 n1=n1-1 def afficher(t1,t2,n): print(t1[0], end =" ") for i in range(1,n) : if t2[i-1]!=t2[i] : print() print(t1[i], end =" ") #programme principal n=saisie_taille() print('remplissage des deux tableaux t1 et t2') remplir(t1,t2,n) # trier les deux tableaux dans un ordre decroissant print('Trier les deux tableaux t1 et t2') tri_bulle_decroissant(t1,t2,n) print('affichage') afficher(t1,t2,n) |
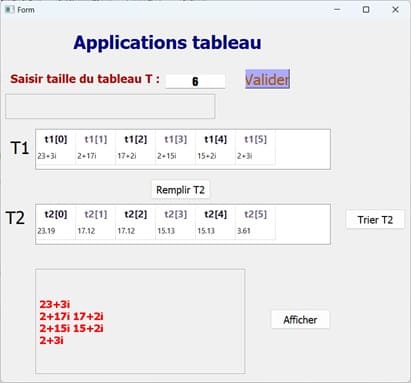
Exécution du programme
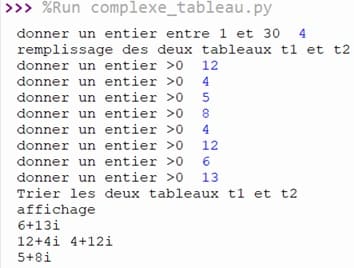
1) Remplissage des deux tableaux
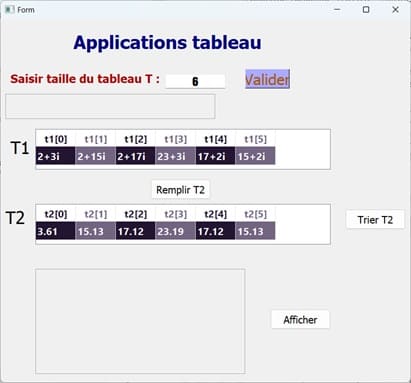
2) Trier les deux tableaux
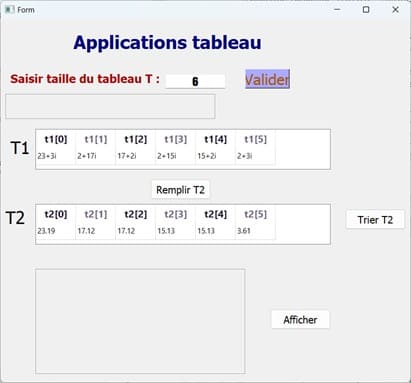
3) Affichage des nombres complexes du tableau T1 en les regroupant par modules similaires.
Solution en Python et Designer QT
Pour résoudre le problème précédent à partir d'une chaîne de caractères en Python, vous pouvez suivre les étapes suivantes :
a- Découper la chaîne de caractères en sous-chaînes.
b- Ajouter chaque sous-chaîne au tableau.
c- Suivre les étapes mentionnées dans partie préceédente
1- Créer l'interface graphique avec Qt Designer
a- Ouvrez Qt Designer et créez un nouveau fichier de type Main Window.
b- Ajoutez ces widgets:
QLineEdit nommé 'ch' pour entrer des entiers .
QPushButton nommé 'remplir_bt' pour exécuter le module createTab afin de remplir le tableau à partir de la chaine 'ch'.
QPushButton nommé 'trier_bt' pour exécuter le module tri_bulle_decroissant.
QPushButton nommé 'afficher_bt' pour exécuter le module afficher_lignes.
QLabel nommé 'msg' pour afficher un message d'erreur si ch est vide ou contient des valeurs non numériques .
QLabel nommé 'tab_label' pour afficher les éléments du tableau t1.
QLabel nommé 'tab2_label' pour afficher les éléments du tableau t2.
QLabel nommé 'ligne_label' pour afficher les nombres complexes du tableau T1 en les regroupant par modules similaires.
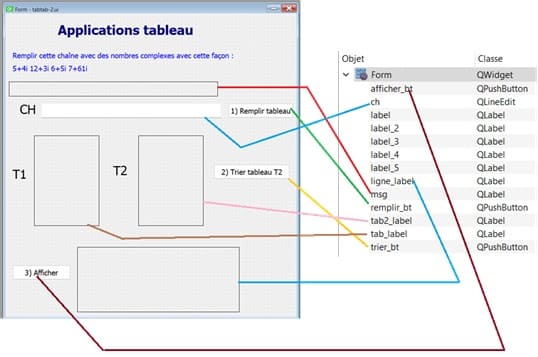
Enregistrez le fichier avec l'extension .ui, par exemple tabtab-2.ui.
2- Créer le script Python pour l'application
Voici un exemple de script Python qui utilise l'interface graphique générée par Qt Designer.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 |
from PyQt5.uic import loadUi from PyQt5 import QtCore, QtGui from PyQt5.QtWidgets import * from PyQt5 import QtCore, QtGui, QtWidgets from numpy import array import math t1=array([str]*30) t2=array([float()]*30) app = QApplication([]) windows = loadUi ("tabtab-2.ui") # Fonction qui supprime des espaces de la chaine des carcatères def supprimer_espaces (ch) : while(ch[0]==' '): # elimnier tous les espaces au début de la chaine ch=ch[1:len(ch)] while(ch[len(ch)-1]==' '): # elimnier tous les espaces a la fin de la chaine ch=ch[0:len(ch)-1] while (ch.find(' ')>0): ch=ch.replace(" ", " ") # remplacer les doubles espaces apar un seul espace return ch def module_complexe(ch): # calculer le module du nombre complexe ch1='' i=0 while i<len(ch): if ('0'<=ch[i]<='9') : ch1=ch1+ch[i] if (ch[i]=='+') : a=int(ch1) ch1='' if (ch[i]=='i') : b=int(ch1) ch1='' i=i+1 return format(math.sqrt(a*a+b*b), '.2f') def tri_bulle_decroissant(t1,t2,n): n1=n permuter=True; while (permuter==True) and ( n1>1) : permuter=False for i in range (0,n1-1): if (t2[i]<t2[i+1]): permuter=True temp2=t2[i] t2[i]=t2[i+1] t2[i+1]=temp2 temp1=t1[i] t1[i]=t1[i+1] t1[i+1]=temp1 n1=n1-1 def afficher_tabs(n): tab='' tab2='' for k in range (n) : tab=tab+ 't1['+str(k)+']= '+ str(t1[k])+ '\n' t2[k]=module_complexe(t1[k]) tab2=tab2+ 't2['+str(k)+']= '+ str(t2[k])+ '\n' #afficher les elements du tableau windows.tab_label.setText(tab) windows.tab2_label.setText(tab2) # Procedure qui remplit un tableau par des nombres complexes a partir d'une chaine des caractère def createTab(): windows.ligne_label.setText(' ') ch = windows.ch.text() global n # taille des deux tableaux if ch=="": windows.msg.setText("Veuillez remplir la chaîne") else: windows.msg.clear() # effacer le message d erreur ch= supprimer_espaces(ch) i=0 j=0 ch1='' # parcourir les caracteres de la chaine while i<len(ch): if ((ch[i]==' ') or (i==len(ch)-1)) : t1[j]=ch1 ch1='' j=j+1 else: ch1=ch1+ch[i] i=i+1 t1[j-1]=t1[j-1]+'i' n=j# pour taille des tableaux afficher_tabs(n) def TrierTab(): n1=n permuter=True; while (permuter==True) and ( n1>1) : permuter=False for i in range (0,n1-1): if (t2[i]<t2[i+1]): permuter=True temp2=t2[i] t2[i]=t2[i+1] t2[i+1]=temp2 temp1=t1[i] t1[i]=t1[i+1] t1[i+1]=temp1 n1=n1-1 afficher_tabs(n) def afficher_lignes(): liste=t1[0]+' ' for i in range(1,n) : if t2[i-1]!=t2[i] : liste=liste+'\n' liste=liste+t1[i]+' ' windows.ligne_label.setText(liste) windows.remplir_bt.clicked.connect ( createTab ) windows.trier_bt.clicked.connect ( TrierTab ) windows.afficher_bt.clicked.connect ( afficher_lignes ) windows.show() app.exec_() |
Exécution du programme
1) Remplissage des deux tableaux
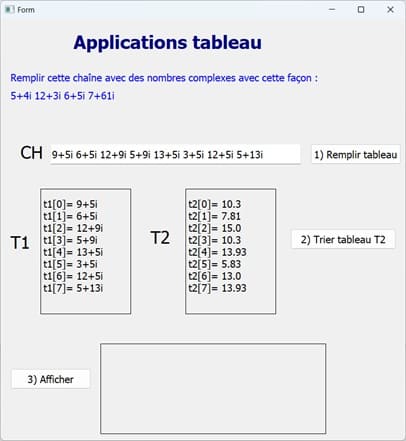
2) Trier les deux tableaux
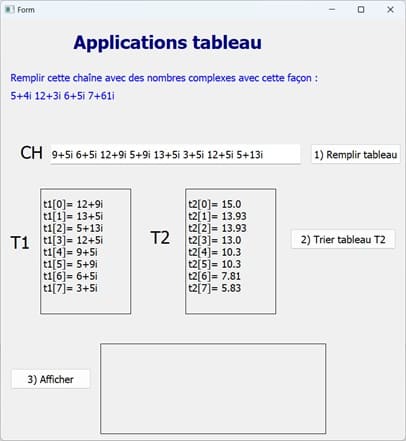
3) Affichage des nombres complexes du tableau T1 en les regroupant par modules similaires.

Vous pouvez voir aussi :
1) des exercices sur les chaînes des caractères
2) des exercices sur les tableaux
3) des sujets Bac pratique
4) des sujets Bac théorique
0 commentaire
laisser un commentaire
Tutoriels récents
Tutoriels populaires

Tutoriels plus commentés



















